python虽然与R一样都可以做数据分析,但是在计量方面较为薄弱,python更像是干脏活,清洗数据用的。现在慢慢的python也有一些在计量的包,比如causalinference,这个包可以做因果推断分析。
下载
安装
!pip3 install causalinference
数据导入
import pandas as pd
df = pd.read_csv('data.csv')
df
Run
| y | istreatment | x1 | x2 | x3 | |
|---|---|---|---|---|---|
| 0 | 4.63639 | 1 | -0.355052 | 0.441348 | 0.908629 |
| 1 | -1.96549 | 0 | -0.81926 | -0.712998 | 0.0375631 |
| 2 | 0.581781 | 0 | 1.39134 | -0.0172917 | -0.804188 |
| 3 | -2.06729 | 0 | -0.831021 | 0.49786 | 0.349555 |
| 4 | 9.54683 | 1 | 1.68232 | 0.608986 | 0.937725 |
数据描述
- x1,x2,x3 协变量(控制变量)
- y 因变量
- istreatment 处置变量D,标注每条数据隶属于treatment或control组。1为treatment, 0为control。
from causalinference import CausalModel
Y = df['y'].values
D = df['istreatment'].values
X = df[['x1', 'x2', 'x3']].values
#CausalModel参数依次为Y, D, X。其中Y为因变量
causal = CausalModel(Y, D, X)
causal
Run
<causalinference.causal.CausalModel at 0x7fd3ad0edee0>
描述性统计分析
print(causal.summary_stats)
Run
Summary Statistics
Controls (N_c=2509) Treated (N_t=2491)
Variable Mean S.d. Mean S.d. Raw-diff
--------------------------------------------------------------------------------
Y -1.012 1.742 4.978 3.068 5.989
Controls (N_c=2509) Treated (N_t=2491)
Variable Mean S.d. Mean S.d. Nor-diff
--------------------------------------------------------------------------------
X0 -0.343 0.940 0.336 0.961 0.714
X1 -0.347 0.936 0.345 0.958 0.730
X2 -0.313 0.940 0.306 0.963 0.650
causal.summary_stats含有的指标字段名
causal.summary_stats.keys()
Run
dict_keys(['N', 'K', 'N_c', 'N_t', 'Y_c_mean', 'Y_t_mean', 'Y_c_sd', 'Y_t_sd', 'rdiff', 'X_c_mean', 'X_t_mean', 'X_c_sd', 'X_t_sd', 'ndiff'])
使用OLS估计处置效应
估计处置效应最简单的方法是使用OLS方法,
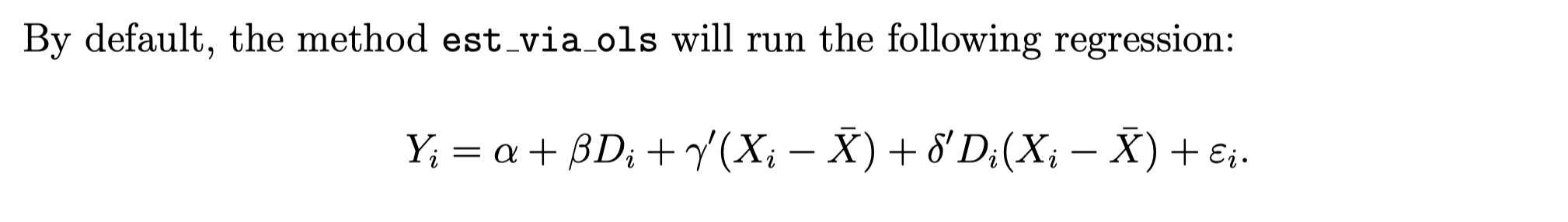
CausalModel.est_via_ols(adj)
该方法有一个参数adj
- adj=0 模型未使用X(协变量)
- adj=1 模型使用了D(是否为处置组)和X(协变量)。
- adj=2 模型使用了D(是否为处置组)、X(协变量)、D与X的交互
- adj默认为2
causal.est_via_ols(adj=2)
print(causal.estimates)
Run
Treatment Effect Estimates: OLS
Est. S.e. z P>|z| [95% Conf. int.]
--------------------------------------------------------------------------------
ATE 3.017 0.034 88.740 0.000 2.950 3.083
ATC 2.031 0.040 51.183 0.000 1.953 2.108
ATT 4.010 0.039 103.964 0.000 3.934 4.086
参数解读
- ATE 平均处置效应(average treatment effect)
- ATC 控制组的平均处置效应(average treatment effect for the controls)
- ATT 处置组的平均处置效应(average treatment effect for the treated)
你们再试试adj设置为0和1分别运行出什么结果
倾向得分估计
我们估计处置效应时,很希望处置组和控制组很类似。比如研究受教育水平对个人收入的影响,其他变量如家庭背景、年龄、地区等协变量存在差异,我们希望控制组和处置组的之间的协变量平衡性尽可能的好,这样两个组就会很像,当对这两个组的受教育水平进行操作时,两个组的收入差异可以认为是受教育水平带来的。
让两个组很像,这里就用到倾向得分估计。
causal.est_propensity_s()
print(causal.propensity)
Run
Estimated Parameters of Propensity Score
Coef. S.e. z P>|z| [95% Conf. int.]
--------------------------------------------------------------------------------
Intercept 0.005 0.035 0.145 0.885 -0.063 0.073
X1 0.999 0.041 24.495 0.000 0.919 1.079
X0 1.000 0.041 24.543 0.000 0.920 1.080
X2 0.933 0.040 23.181 0.000 0.855 1.012
分层方法估计处置效应
倾向得分估计,让两个组尽量相似,但实际上这个相似值范围有点大。比如假设受教育水平对个人收入的影响,身高、体重等颜值信息(协变量)其实对收入也是有影响的,那么就应该对人群进行分层,不同颜值水平下受教育水平对个人收入的影响。
分层方法估计CausalModel.stratify_s 自动选择协变量
causal.stratify_s()
print(causal.strata)
Run
Stratification Summary
Propensity Score Sample Size Ave. Propensity Outcome
Stratum Min. Max. Controls Treated Controls Treated Raw-diff
--------------------------------------------------------------------------------
1 0.001 0.043 153 5 0.024 0.029 -0.049
2 0.043 0.069 148 8 0.056 0.059 0.142
3 0.070 0.118 283 29 0.093 0.092 0.953
4 0.119 0.178 268 45 0.147 0.147 1.154
5 0.178 0.240 247 65 0.208 0.210 1.728
6 0.240 0.361 451 174 0.299 0.300 2.093
7 0.361 0.427 196 117 0.393 0.395 2.406
8 0.427 0.499 153 159 0.465 0.464 2.868
9 0.499 0.532 82 75 0.515 0.515 2.973
10 0.532 0.568 65 91 0.551 0.553 3.259
11 0.568 0.630 114 198 0.600 0.601 3.456
12 0.630 0.758 180 445 0.693 0.696 3.918
13 0.758 0.818 77 236 0.787 0.789 4.503
14 0.818 0.876 57 255 0.845 0.849 4.937
15 0.876 0.933 23 289 0.904 0.904 5.171
16 0.933 0.998 12 300 0.957 0.963 6.822

