作者: Spectator
一、PPS
**Predictive Power Score(PPS)**是一种不对称、与数据类型无关的评分,可以检测两个变量之间的线性或非线性关系。分数范围从 0(无预测能力)到 1(完美预测能力)。 与Pearson相关性不同,它可以处理非线性关系、分类数据和不对称关系,例如变量 A 对变量 B 的影响大于变量 B 对变量 A 的影响。
二、问题
相关性分析 是对具有相关性的两个或多个变量元素进行研究,以衡量它们之间的相关性程度。当我们不清楚数据集特征的含义时,通常可以直接进行相关性分析,以检查特征之间的相关系数。
在统计学中,常用的方法是使用 皮尔逊积矩相关系数(Pearson product-moment correlation coefficient)来度量两组数据变量X和Y之间的线性相关性。这个系数是协方差除以它们的标准差的乘积,因此它实际上是协方差的标准化度量,其结果始终在 -1 和 1 之间。系数为1表示X和Y之间有很强的线性关系,所有数据点都近似位于一条直线上,Y随着X的增加而增加。系数为-1表示所有数据点都位于一条直线上,但Y随着X的增加而减少。系数为0表示两个变量之间没有线性关系。两个变量之间的皮尔逊相关系数定义为两个变量的协方差除以它们标准差的乘积:

由于皮尔逊相关系数是度量变量之间的线性关系的,那么就无法检测到数据之间的非线性关系,如下图的示例。

由皮尔逊相关系数定义的公式可知,皮尔逊相关系数是对称的,即P(A,B) = P(B,A), 但是在真实世界中,特征之间的关系往往是不对称的,例如:我可以根据你的手机号推断你是哪个城市的,但是不能根据你的城市推断出你的手机号。 同时我们也会发现,当特征是非数值向量时,例如是Onehot向量时,皮尔逊相关系数是没有办法对齐进行处理的。
综上所述,常用的皮尔逊相关系数存在以下问题:
- 只能度量线性关系;
- 度量的关系是对称的;
- 不能处理非数值向量之间的关系。
计算“x 预测 y”的PPS得分
- 分数始终介于 0 到 1 之间,并且与数据类型无关。
- 得分 0 意味着 x 列无法比朴素基线模型更好地预测 y 列。
- 得分 1 意味着 x 列可以在给定模型的情况下完美预测 y 列。
- 0 到 1 之间的分数表示模型与基线模型相比所实现的潜在预测能力的比率。
在 Python 和 R 中均有pps的库, 分别是 ppscore库 和 ppsr 包, 今天以 ppsr为例分享。
三、ppsr用法
该ppsr软件包有四个主要函数来计算 PPS:
ppsr::score()计算 xy PPSppsr::score_matrix()计算所有 XY PPS,并将它们显示在矩阵中ppsr::visualize_ppspps得分矩阵ppsr::visualize_correlations相关矩阵
其中x和y代表单个预测变量/目标,并且X和 Y代表给定数据集中的所有预测变量/目标。
3.1 安装
在R中安装ppsr,打开命令行, 执行
install.packages('ppsr')
3.2 score()
score()计算单个目标和预测变量的 PPS
例如,使用决策树回归模型计算 x预测y 的PPS……
ppsr::score(iris, x = 'Sepal.Length', y = 'Petal.Length', algorithm = 'tree')[['pps']]
#> [1] 0.6160836
使用广义线性回归模型计算 x预测y 的PPS……
ppsr::score(iris, x = 'Sepal.Length', y = 'Petal.Length', algorithm = 'glm')[['pps']]
#> [1] 0.5441131
3.3 score_matrix()
类似于Pearson相关矩阵
ppsr::score_matrix(df = iris)
#> Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> Sepal.Length 1.00000000 0.04632352 0.5491398 0.4127668 0.4075487
#> Sepal.Width 0.06790301 1.00000000 0.2376991 0.2174659 0.2012876
#> Petal.Length 0.61608360 0.24263851 1.0000000 0.7917512 0.7904907
#> Petal.Width 0.48735314 0.20124105 0.7437845 1.0000000 0.7561113
#> Species 0.55918638 0.31344008 0.9167580 0.9398532 1.0000000
3.4 可视化
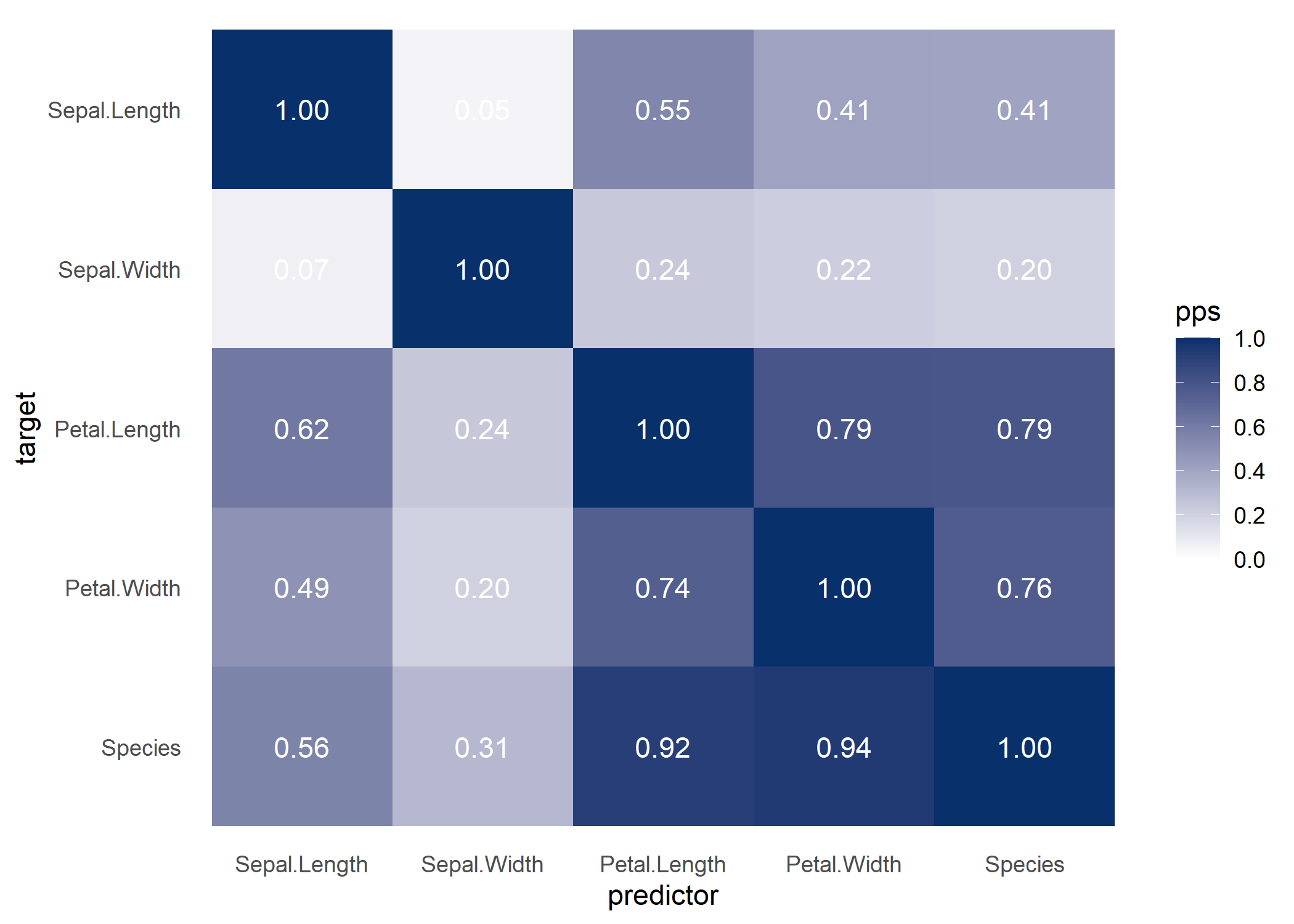
pps得分矩阵
ppsr::visualize_pps(df = iris)

相关矩阵
ppsr::visualize_correlations(df = iris)

并排生成 PPS 和相关矩阵,以便于比较。
ppsr::visualize_both(df = iris)

四、PPS应用
PPS的应用,了解了 PPS 的优点之后,我们来看看在现实生活中我们可以在哪些地方使用 PPS:
- 查找数据中的模式: PPS 查找相关性发现的每一个关系,甚至更多。因此,您可以使用 PPS 矩阵替代相关矩阵来检测和理解数据中的线性或非线性模式。使用始终在 0 到 1 之间的单个分数跨数据类型是可能的。
- 特征选择:除了您通常的特征选择机制外,您还可以使用预测能力得分来为您的目标列找到好的预测变量。此外,您可以消除仅添加随机噪声的功能。这些特征有时在特征重要性指标上仍然得分很高。此外,您可以消除其他特征可以预测的特征,因为它们不会添加新信息。此外,您可以识别 PPS 矩阵中的相互预测特征对——这包括强相关特征,但也将检测非线性关系。
- 检测信息泄露:使用 PPS 矩阵检测变量之间的信息泄露——即使信息泄露是通过其他变量介导的。
- 数据规范化:通过将 PPS 矩阵解释为有向图来查找数据中的实体结构。当数据包含以前未知的潜在结构时,这可能会令人惊讶。